JavaScript遍历树的两种方式

JavaScript遍历树的两种方式

十一月 04, 2020

树

树是n个节点的集合，树有且仅有一个顶点，被称为根节点，从根开始定义，根为第一层，根的直接子节点为第二层，依此类推，树中节点的最大层数被称为树的深度或高度。

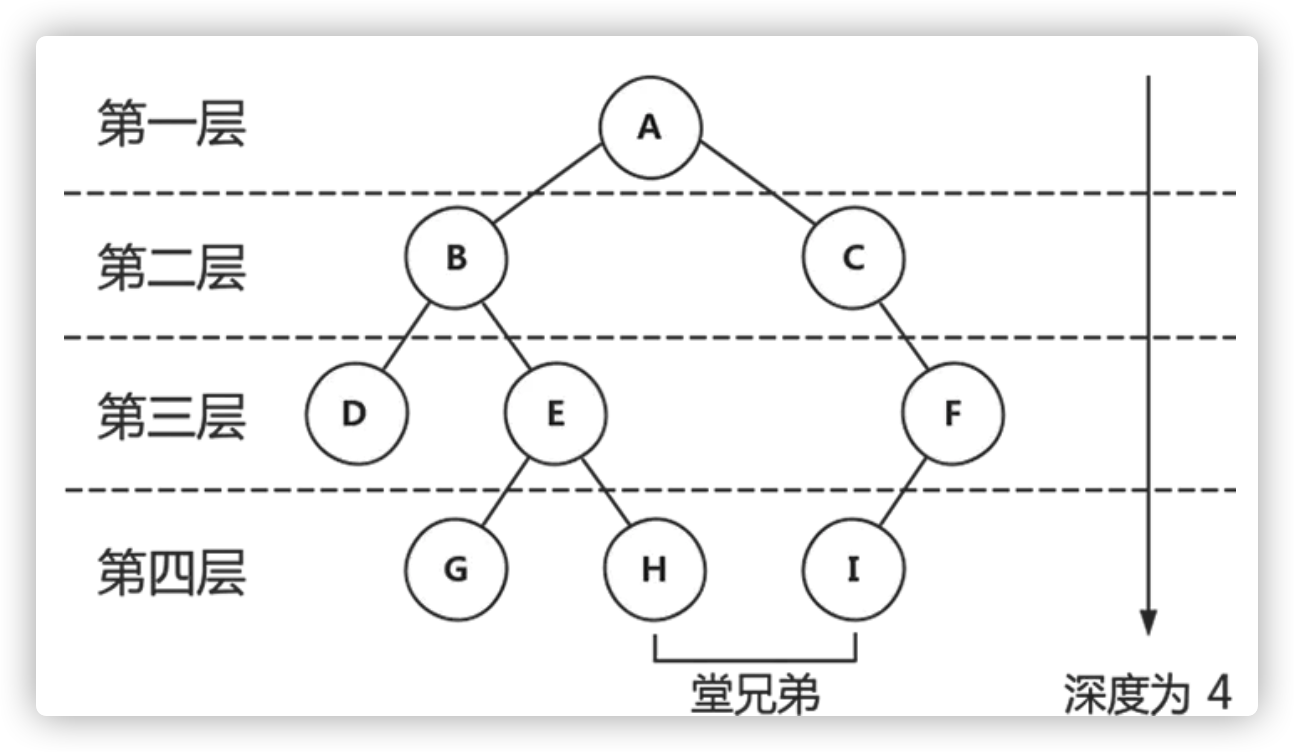
iShot2020-11-04 17.25.44

树的遍历

在对树进行遍历的时候，可以分为先序，中序和后序，按照遍历方式可分为深度优先遍历（DFS）和广度优先遍历（BFS），详细如图：

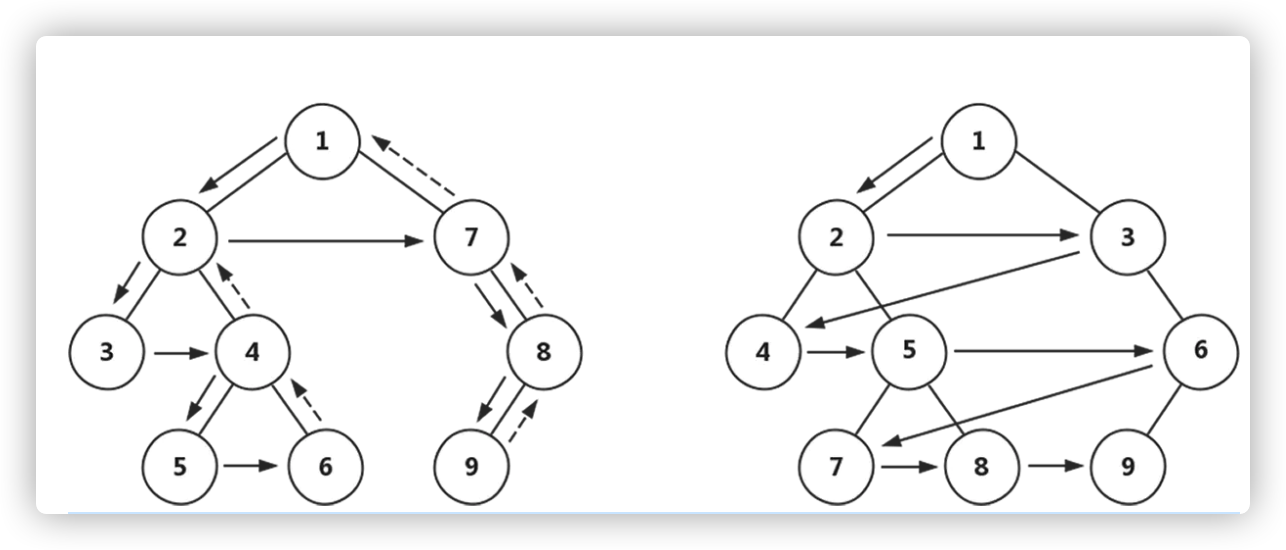
iShot2020-11-04 17.21.41

首先我们构造一个树结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
const tree = [
  {
    id: 1,
    children: [
      {
        id: 2,
        children: [{ id: 3 }, { id: 4, children: [{ id: 5 }, { id: 6 }] }],
      },
    ],
  },
  {
    id: 7,
    children: [
      {
        id: 8,
        children: [{ id: 9 }],
      },
    ],
  },
]

深度优先遍历

深度优先搜索（depth first search），从图中也可以看出来，是从根节点开始，沿树的深度进行搜索，尽可能深的搜索分支。当节点所在的边都已经搜多过，则回溯到上一个节点，再搜索其余的边。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
const depthSearchWithRecursive = (source) => {
  const result = [] // 存放结果的数组
  // 递归方法
  const dfs = (data) => {
    // 遍历数组
    data.forEach((element) => {
      // 将当前节点 id 存放进结果
      result.push(element.id)
      // 如果当前节点有子节点，则递归调用
      if (element.children && element.children.length > 0) {
        dfs(element.children)
      }
    })
  }
  // 开始搜索
  dfs(source)
  return result
}

const depthSearchWithoutRecursive = (source) => {
  const result = [] // 存放结果的数组
  // 当前栈内为全部数组
  const stack = JSON.parse(JSON.stringify(source))
  // 循环条件，栈不为空
  while (stack.length !== 0) {
    // 最上层节点出栈
    const node = stack.shift()
    // 存放节点
    result.push(node.id)
    // 如果该节点有子节点，将子节点存入栈中，继续下一次循环
    const len = node.children && node.children.length
    for (let i = len - 1; i >= 0; i -= 1) {
      stack.unshift(node.children[i])
    }
  }
  return result
}

console.log(depthSearchWithRecursive(tree)) // [1, 2, 3, 4, 5, 6, 7, 8, 9]
console.log(depthSearchWithoutRecursive(tree)) // [1, 2, 3, 4, 5, 6, 7, 8, 9]

广度优先遍历

广度优先搜索（breadth first search），从图中也可以看出来，是从根节点开始，沿树的宽度进行搜索，如果所有节点都被访问，则算法中止。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
const breadthSearch = source => {
  const result = []; // 存放结果的数组
  // 当前队列为全部数据
  const queue = JSON.parse(JSON.stringify(source));
  // 循环条件，队列不为空
  while (queue.length > 0) {
    // 第一个节点出队列
    const node = queue.shift();
    // 存放结果数组
    result.push(node.id);
    // 当前节点有子节点则将子节点存入队列，继续下一次的循环
    const len = node.children && node.children.length;
    for (let i = 0; i < len; i += 1) {
      queue.push(node.children[i]);
    }
  }
  return result;
};

console.log(breadthSearch(tree)) // [1, 7, 2, 8, 3, 4, 9, 5, 6]